elektorotechnika

Prúd

Elektrický prúd je pohyb voľných nosičov elektrického náboja elektrónov medzi atómami vodiča. (záporných elektrónov). Elektróny sú nositeľmi záporného náboja a preto sa v skutočnosti pohybujú od zápornej svorky zdroja ku kladnej svorke. Smer prúdu však kreslíme však opačne, lebo sme tento smer prúdu začali na základe všeobecnej dohody takto označovať. Elektrický prúd tečie od kladného k zápornému pólu zdroja, i keď tok elektrónov v skutočnosti opačný.

--

Merný a  odpor

Kryštalografická štruktúra materiálov je rozdielna, čo sa prejavuje aj odlišným elektrickým odporom. Z týchto dôvodov určitý kov vedie elektrický prúd výborne (napr. zlato , striebro), iný horšie (napr. železo, olovo a pod.). hovoríme, že materiály majú rozličný merný odpor (špecifický odpor).

Merný odpor je teda odpor vodiča jednotkovej dĺžky a jednotkového prierezu.

Merný elektrický odpor ρ alebo rezistivita alebo špecifický elektrický odpor je fyzikálna veličina, vyjadrujúca elektrický odpor vodiča dĺžky 1 m o priereze 1 m².

Merný elektrický odpor je materiálová konštanta, charakterizujúca elektrickú vodivosť látky. Čím väčší je merný elektrický odpor, tým menšia je vodivosť danej látky.

                       

Pokiaľ poznáme dlžku, prierez a merný elektrický odpor vodiča z homogénneho materiálu, jeho odpor vypočítame zo vzťahu:

R- celkový elektrický odpor vodiča v  Ω

ρ- merný odpor materiálu  udávaný v Ω.mm²/m

l- dížka vodiča v m

S- prierez vodiča mm²

Ideálny a skutočný zdroj

Ideálny napäťový zdroj je taký, ktorý má nulový vnútorný odpor R_i. Takýto zdroj sa vplyvom veľkosti zaťažovacieho prúdu nemení svorkové napätie U_S.

Skutočný napäťový zdroj má však určitý vnútorný odpor R_i , ktorý spôsobuje, že napätie na jeho svorkách vplyvom zvyšovania zaťažovacieho prúdu klesá. Spôsobuje to úbytok napätia na jeho vnútornom odpore U_i = R_i . I_Z .

Ak napäťový zdroj nezaťažíme žiadnym zaťažovacím prúdom (I_Z = 0), potom napätie na svorkách zdroja U_S sa rovná vnútornému napätiu U_i , ktoré nazývame napätie naprázdno U_o.

Kirchhoffov zákon 

Súčet prúdov vtekajúcich do uzla sa rovná súčtu prúdov vytekajúcich z uzla.

                                   I₁  + I₂ = I₃ + I₄ + I₅ 

Coulombov zákon 

-vyjadruje veľkosť sily, ktorou na seba pôsobia dva statické bodové náboje . Bodový náboj predstavuje  elektricky nabité teleso, ktorého rozmery môžeme zanedbať.

Podľa presných pokusov dva bodové náboje pôsobia na seba navzájom silou F, ktorá je priamo úmerná ich súčinu a nepriamo úmerná druhej mocnine ich vzdialenosti.

Q₁ , Q₂ – bodové náboje

r-      vzájomná vzdialenosť bodových nábojov

Kapacita a kondenzátory:

Kapacita je schopnosť vodiča nahromadiť len určité množstvo naáboja pri určitom potenciály, prípadne napätí.

 Jednotkou kapacity je farad, značka F, je to kapacita vodiča, na ktorom by pri napätí 1V nahromadil náboj 1C (coulomb).

Kondenzátor je elektrická súčiastka, ktorá sa skladá z dvoch vodivých platní oddelených dielektrikom. Dielektrikum môže byť napríklad sľuda, papier, vzduch, pvc a pod.

Kapacitu doskového rovinného kondenzátora je možné vyjadriť vzťahom:

Vzťah pre kapacitu doskového kondenzátora: povedať slovne od čoho závisí veľkosť kapacity doskového kondenzátora

ε- permitivita dielektrika, je to číslo, ktoré vyjadruje vlastnosť dielektrika ε= ε_r . ε_o

ε_r- relatívna permitivita

ε_o – permitivita vákua

S- plocha dosiek (prierez dielektrika)

d- vzdialenosť dosiek

Elektromagneticke pole:

Okolo vodiča, cez ktorý prechádza prúd, vzniká magnetické pole, ktoré sa znázorňuje siločiarami majúcimi tvar kružníc či elíps. Ich smer závisí od smeru prúdu tečúceho cez vodič. K určeniu smeru siločiar sa využíva

Ampérovo pravidlo pravej ruky: Ak zovrieme vodič prúdu do pravej ruky tak, aby palec ukazoval smer prúdu, konce prstov udávajú smer siločiar magnetického poľa. 

O prítomnosti magnetického poľa v okolí vodiča sa môžme presvedčiť priblížením magnetky k vodiču. Ak ju postavíme kolmo na vodič, pootočí sa jej severný koniec v magnetickom poli do smeru magnetických siločiar (Obr. 2), ak ju postavíme rovnobežne s vodičom prúdu, vychýli sa podľa Ampérovho pravidla pravej ruky. Nikdy sa však nevychýli o celých 180°, pretože na ňu pôsobí aj magnetické pole Zeme.

Valcová cievka so závitmi v tesnej blízkosti seba má pri prechode prúdu vo vnútri cievky homogénne pole.

Smer tohto poľa určíme podľa pravidla pravej ruky:

Ak uchopíme cievku do dlane tak, že prsty ukazujú smer prúdu jednotlivými závitmi, vystretý palec udáva serverný pól cievky.

Hodnoty

Okamžitá hodnota – u(t). Je hodnota, ktorú daná veličina nadobúda v danom okamihu. Pri striedavých veličinách sa

okamžitá hodnota v čase neustále mení. Štandardne sa označuje malými písanými písmenami.

Efektívna hodnota – Uef. Efektívna hodnota striedavého napätia je taká hodnota jednosmerného stacionárneho

napätia, ktorá vytvorí na ideálnom rezistore počas jednej periódy rovnaké množstvo tepla, ako uvažované striedavé

napätie.

Stredná hodnota – Ustr. Stredná hodnota striedavého napätia je taká hodnota jednosmerného stacionárneho napätia,

pri ktorej sa prenesie rovnaké množstvo náboja ako pri uvažovanom jednosmernom napätí za jednu periódu.

Pre harmonické veličiny je stredná hodnota rovná 0.

Maximálna hodnota – Umax. Maximálna amplitúda striedavého napätia je hodnota od špičky ku špičke delená dvoma.

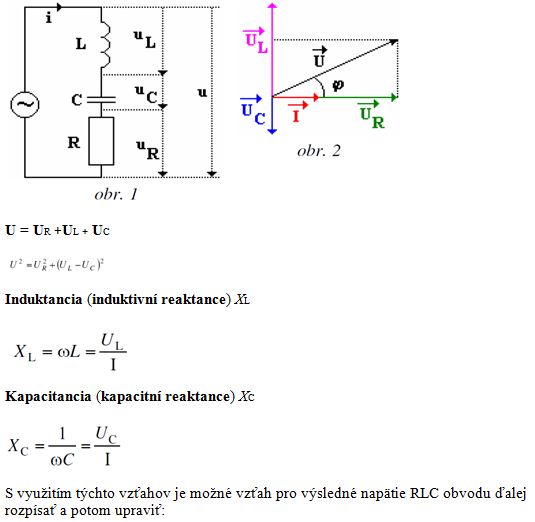
Fázorový diagram sériového RLC obvodu a Výpočet impedancie 

Generátor trojfázovej sústavy do hviezdy

Trojfázový spotrebič zapojíme na všetky tri fázy a nulový vodič, a tým získame výkon akoby troch jednofázových spotrebičov, kde každý z nich je privedený na napätie 230V.

Budeme využívať fázové napätie, čo je rozdiel potenciálu jednej fázy a nulového vodiča.

Spotrebič zapojíme medzi dve fázy a obvod sa bude uzatvárať medzi fázami.

Budeme využívať združené napätie, čo je vektorový súčet resp. rozdiel dvoch fázových napätí.

Pri pripojení spotrebiča na združené napätie sa bude prúd uzatvárať medzi fázami (nie cez nulový vodič):

Vzťah medzi združeným a fázovým napätím:

Z uvedeného vyplýva, že vzťah medzi združeným napätím U_Z a fázovým napätím U_f je:

Uz=(odmocnina z cisla 3 ) * Uf

Spojenie vinutí trojfázového generátora (zdroja) do hviezdy nám umožňuje využívať dva druhy napätia (fázové a združené). To znamená, že toto zapojenie nám umožňuje získanie väčšieho napätia. V konečnom dôsledku spájaním zdroja trojfázového napätia či už do hviezdy alebo do trojuholníka, umožňuje získanie väčších napätí alebo prúdov, čiže výkonu. V našej rozvodnej sieti sú nasledovné hodnoty napätí :

U_f = 230V, U_Z = 400V---sú to efektívne hodnoty napätí

Výkon

P - jednofázový činný výkon (reálny, tepelný výkon), W

Q - jednofázový jalový výkon (reaktančný, imaginárny výkon, VAr

S - jednofázový zdanlivý výkon (celkový výkon), VA

cos j - účinník striedavého prúdu, -

U - efektívna hodnota striedavého napätia, V

I - efektívna hodnota striedavého prúdu, A

Praktické využitie seriového rezonančného R-L-C obvodu:

- vo vf technike, kde sa pracuje s frekvenciami radove kHz a MHz

- dlhy priamy vodič, ktory služi ako vysielacia antenna radiovych vĺn, predstavuje sice nepatrnú indukčnosť a kapacitu, ale pri vf prude nema už X_L a X_C zanedbateľne (C najmenej pF))pri rezonančnej frekvencii, na ktoru je antena naladena pre vysielaci signal, ma obvod najmenšiu impedanciu a signal nim veľmi ľahko prejde. Vo forme elektromagnetickeho vlnenia sa vyžiari do eteru.

Prakticke využitie paralelneho rezonančneho obvodu:

vf technika:

ak pripojime paralelny rezonančny obvod (ma maximalnu impedanciu) na antenny vstup radioprijimača, prud indukovany v antene zapričini najvačšie napatie – prijimaci signal – pre tuto frekvenciu, na ktoru je obvod prave naladeny.

Napatia ďaľšich frekvencii – inych vysielacich stanic – budu male, pretože impedancia obvodu pre tieto frekvencie je veľmi mala

silnoprudova elektrotechnika:

veľke indukčne elektricke spotrebiče (tlmivky, motory) zaťažuju vedenie zdanlivym – jalovym –

vykonom. Podľa vysledneho prudu, ktory je dany geometrickym sučtom činneho a jaloveho prudu, treba dimenzovať prierez vedenia vzhľadom na straty, ktore zavisia od štvorca tohto prudu.

Ak ku takemuto indukčnemu spotrebiču pripojime paralelne kondenzator približne takej hodnoty,že spotrebič spolu s kondenzatorom bude predstavovať rezonančny obvod, vedenim potečie len činny prud (menši, čiže aj prierez stači menši), kym jalovu energiu bude spotrebiču dodavať

kondenzator. Straty prenosom sa zmenšia.

Takyto kondenzator sa nazyva kompenzator , lebo kompenzuje učinnik v obvode (cosφ).

Z ekonomickych dovodov nekompenzujeme fazovy posuv nikdy až na nulu – asi by to ani nešlo.

Pre prax stači cosφ = 0,85-0,95. Nie sme teda v uplnej rezonancii.

https://docs.google.com/open?id=0B6smGPB8A5ISOGdjN0NaRHBYSWs
https://docs.google.com/open?id=0B6smGPB8A5ISOGdjN0NaRHBYSWs